Matematička gimnazija - Forum Matematičke gimnazije -> Geometrija 7 Razred Sm

Matematička gimnazija - zvanična prezentacija Viva fizika

Početna strana Pravilnik Uputstvo za LaTeX

Dragi clanovi i posetioci foruma,

Mozda ce vam ova brojka zvucati neverovatno, ali Forum Matematicke gimnazije postoji vec vise 6 godina - od januara 2006. godine, ako zelimo da budemo precizni.

Sa vise od 1.000 clanova, 4.000 tema i 100.000 poruka predstavlja najvecu zajednicu orijentisanu ka Matematickoj gimnaziji i ucinio je nase srednjoskolske dane barem iole zanimljivijima. Ne samo da je bio mesto za visokointelektualne razgovore ucenika Matematicke gimnazije, vec i forum na koji smo dolazili da se druzimo sa ljudima iz cele Srbije, pa i regiona. Verujem da ne govorim samo u nase ime kada kazem da su ovde nastala mnoga poznanstva koja su se kasnije dalje razvijala u "pravom svetu".

Nazalost, ta idilicna vremena su sada iza nas. Tokom poslednjih nekoliko godina Internet u regionu je doziveo vrtoglav razvoj, i potreba za ovakvim forumima vise ne postoji. Pojavile su se socijalne mreze kao sto su Facebook i Twitter, i komunikacija je na mnogo visem nivou. Forum, iako pun korisnih informacija, vise ne sluzi svojoj prvobitnoj nameni.

Iz tog razloga, teska srca smo doneli odluku da Forum Matematicke gimnazije prestane sa radom. Od danas registracije na forumu nece biti moguce, ali ce sve poruke i dalje biti dostupne za pregled. Takodje, od prvog septembra forum vise nece biti dostupan na adresi mg-forum.net, ali ce se arhivi i dalje moci pristupiti preko adrese bozidarevic.com/mgforum . Takodje bismo zeleli da iskoristimo priliku i da uputimo sve bivse ucenike na Alumni Matematicke gimnazije - almagi.mg.edu.rs.

Hvala svima koji su ucestvovali u diskusijama i koji su pomogli da ovaj forum bude jedno prijatno mesto.

Administratorski tim MG Foruma

Outline · [ Standard ] · Linear+

Geometrija 7 Razred Sm, Pomooooocccc.....

Track this topic | Email this topic | Print this topic

dexkg	Apr 8 2008, 12:38 AM Post #1
Group: Članovi Joined: 8-April 08 Member No.: 1.000 Status: Van MGa Ime i prezime: Dejan Anicic Škola/Razred: Visoka skola strukovnih studija Cacak-Informatika	Molim Vas za pomoc oko resavanja sledecih zadataka. Naime ovo su zadaci iz pismene koju sam ja slabo uradio e sad ja sam bio druga grupa i to je pismena b a nabavio sam zadatke i iz prve grupe pismena a. Molim vas da mi posaljete resenja , za postupak rada bilo bi super, naravno ako moze. P.S. Pomozite molim Vas. POlgedajte resenja pismene b sto sam uradio ,pismenu a radim sutra, nisam siguran u tacnost zadataka. Vezbao sam iz krugove zbirke, ali ovi zadaci su mi bili na kontrolnom. Pomoc....Hvala unapred This post has been edited by dexkg: Apr 8 2008, 12:39 AM Attached thumbnail(s)

pyost	Apr 8 2008, 07:58 AM Post #2
Deus Ex Makina Group: Administratori Joined: 25-January 06 From: Beograd Member No.: 2 Status: Bivši učenik MGa Škola/Razred: RAF	1. Obim kruga je $\ 2r\pi\ =\ 31m4cm$ (r je 5cm, 2r je precnik od 10cm) .Da bi dobili duzinu kruznog luka, mozemo da posmatramo odnos (pun krug ima 360°, jelte) $\frac{22,5^o}{360^o} = \frac{x}{31,4cm}$ $x = \frac{31,4cm * 22,5^o}{360^o}$ $x = 1,9625cm = 0,625\pi cm$ 2. Imamo da je obim veceg kruga $10\pi cm$ , sto ce reci da je njegov poluprecnik $5cm$ , a poluprecnik manjeg kruga $4cm$ . Dakle: $P = (5cm)^2\pi - (4cm)^2\pi\ =>\ P = 9\pi\ cm^2$ 3. Ako posmatramo polovinu tetive (mrzi me da crtam), ona je duzine $2\sqrt3$ , i kateta je pravouglom trouglu koji gradi sa poluprecnikom kruga. $r = 4cm$ $\frac t 2 = 2\sqrt3cm$ $\frac t 2 = r * \frac{\sqrt3}{2}$ Iz toga mozemo zakljuciti da je ugao naspram polovine tetive 60°, pa je ugao koji zahvata cela tetiva 120°, odnosno 1/3 kruga. Samim tim, trazena povrsina je: $P = \frac13 r^2\pi = 16,747 cm^2$ 4. Neosenceni delovi kvadrata se dobiju kada se od povrsine kvadrata oduzmu ona dva neosencena dela. Jedan neosencen deo ima povrsinu = povrsina kvadrata - povrsina 1/4 kruga poluprecnika a $P = a^2 - 2[a^2 - \frac14 a^2\pi]$ Kada se to sredi, dobije se: $P = a^2(\frac12\pi - 1)$ 5. Ako tetive AB i BC grade prav ugao, to znaci da je AC poluprecnik tog kruga (svi trouglovi konstruisani "nad" precnikom su pravougli). Preko pitagorine teoreme se dobije da je precnik kruga 13cm, odnosno $r = 6,5cm$ $P = r^2\pi = 132,665cm^2\ \ O = 2r\pi = 40,82cm$ A sesti zadatak ne znam kako se radi -------------------- Baby, it's a violent world. Registrovani korisnik Linuxa broj 460770 [Ubuntu 7.10]

dexkg	Apr 8 2008, 08:28 AM Post #3
Group: Članovi Joined: 8-April 08 Member No.: 1.000 Status: Van MGa Ime i prezime: Dejan Anicic Škola/Razred: Visoka skola strukovnih studija Cacak-Informatika	Hvala puno, pokusacu da primenim ovo sto si napisao. Vezbam i dalje. nije mi najasniji ovaj treci zadatak iz pismena b. Molim te pogledaj treci zadatak iz pismena b, samo jos njega , ne snalazim se najbolje sa istim This post has been edited by dexkg: Apr 8 2008, 08:34 AM

LoshMeeBre	Apr 8 2008, 08:30 AM Post #4
Neko mudo Group: Članovi Joined: 28-January 06 From: MunZe Member No.: 3 Status: Bivši učenik MGa Ime i prezime: Milos Vucenovic Škola/Razred: Student ETFa	Boza sav srecan kad USPE da resi neki zadatak Uzmi neki nas... --------------------

pyost	Apr 8 2008, 08:32 AM Post #5
Deus Ex Makina Group: Administratori Joined: 25-January 06 From: Beograd Member No.: 2 Status: Bivši učenik MGa Škola/Razred: RAF	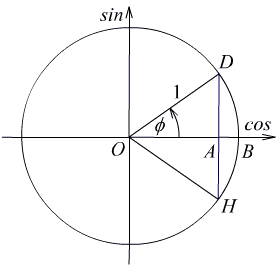OD je poluprecnik, i to je hipotenuza trougla ODA, a DA je polovina tetive, to je krak. Zbog: $DA = \frac{\sqrt3}{2}OD$ Mozemo zakljuciti (pod pretpostavkom da ste to radili - kateta naspram ugla od 30° je polovina hipotenuze, a ako je naspram 60° onda vazi ovaj odnos) da je ugao DAO = 60°, pa je samim tim ugao DAH = 120°, sto je tacno 1/3 kruga -------------------- Baby, it's a violent world. Registrovani korisnik Linuxa broj 460770 [Ubuntu 7.10]

dexkg	Apr 8 2008, 08:44 AM Post #6
Group: Članovi Joined: 8-April 08 Member No.: 1.000 Status: Van MGa Ime i prezime: Dejan Anicic Škola/Razred: Visoka skola strukovnih studija Cacak-Informatika	QUOTE(pyost @ Apr 8 2008, 08:32 AM) OD je poluprecnik, i to je hipotenuza trougla ODA, a DA je polovina tetive, to je krak. Zbog: $DA = \frac{\sqrt3}{2}OD$ Mozemo zakljuciti (pod pretpostavkom da ste to radili - kateta naspram ugla od 30° je polovina hipotenuze, a ako je naspram 60° onda vazi ovaj odnos) da je ugao DAO = 60°, pa je samim tim ugao DAH = 120°, sto je tacno 1/3 kruga Uh ovo mi bas nije najasnije, evo sada radim 5-ti zadatak iz pismene a, ostali nam se poklapaju This post has been edited by dexkg: Apr 8 2008, 08:44 AM

pyost	Apr 8 2008, 08:45 AM Post #7
Deus Ex Makina Group: Administratori Joined: 25-January 06 From: Beograd Member No.: 2 Status: Bivši učenik MGa Škola/Razred: RAF	E pa ja ne mogu bolje da objasnim Ne znam, meni je to ocigledno -------------------- Baby, it's a violent world. Registrovani korisnik Linuxa broj 460770 [Ubuntu 7.10]

dexkg	Apr 8 2008, 08:47 AM Post #8
Group: Članovi Joined: 8-April 08 Member No.: 1.000 Status: Van MGa Ime i prezime: Dejan Anicic Škola/Razred: Visoka skola strukovnih studija Cacak-Informatika	QUOTE(pyost @ Apr 8 2008, 08:45 AM) E pa ja ne mogu bolje da objasnim Ne znam, meni je to ocigledno Ma ok hvala ti i na ovome do sada...puno mi je znacilo, ako se nesto setis sto bi mi jos pomoglo postavi molim te....pozzzz

Nostradamus	Apr 8 2008, 12:14 PM Post #9
Group: Članovi Joined: 5-November 07 From: Bg Member No.: 747 Status: Bivši učenik MGa	E za ovaj jedan 6 (prva grupa) samo nadovezi duz duzine kao CD na BD (u tacki B,) i lako se pokaze da su trouglovi ACD i ABC' (BC' ti je ta nadovezana duz ), jer odmah imas dve ivice treba da se pokaze da je ugao izmedju njih isti, a to se isto lako vidi. Onda je trougao BC'D jednakostranican sto je i trebalo da se pokaze. (Jbg. ne umem sliku da ubacim, a tako bi bilo lakse). E a u ovom drugom sta ce ti ono D, kad se nigde ne pominje, a simetrala ugla i naspramna stranica se uvek seku? Nije bas umetnicko delo, ali valjda se vidi nesto This post has been edited by Nostradamus: Apr 8 2008, 12:33 PM Attached thumbnail(s) -------------------- $(a,b) \sim (c,d) \Leftrightarrow (a - c) \in \mathbb{Z} \wedge (b - d) \in \mathbb{Z}$ $\mathbb{T}^2\equiv\mathbb{R}^2/\sim$

dexkg	Apr 8 2008, 12:21 PM Post #10
Group: Članovi Joined: 8-April 08 Member No.: 1.000 Status: Van MGa Ime i prezime: Dejan Anicic Škola/Razred: Visoka skola strukovnih studija Cacak-Informatika	[quote=Nostradamus,Apr 8 2008, 12:14 PM] (Jbg. ne umem sliku da ubacim, a tako bi bilo lakse). edit na tvojoj poruci pa Imas dole pri dnu attachments preko toga ubaci sliku. pozzz This post has been edited by dexkg: Apr 8 2008, 12:22 PM

Nostradamus	Apr 8 2008, 06:17 PM Post #11
Group: Članovi Joined: 5-November 07 From: Bg Member No.: 747 Status: Bivši učenik MGa	U ovom druom mora da bude jednakostranican, jer upisani krug dodiruje trougao u sredistima ivica, i zato sto su odsecci tangenta jednaki. -------------------- $(a,b) \sim (c,d) \Leftrightarrow (a - c) \in \mathbb{Z} \wedge (b - d) \in \mathbb{Z}$ $\mathbb{T}^2\equiv\mathbb{R}^2/\sim$

dexkg	Apr 8 2008, 10:47 PM Post #12
Group: Članovi Joined: 8-April 08 Member No.: 1.000 Status: Van MGa Ime i prezime: Dejan Anicic Škola/Razred: Visoka skola strukovnih studija Cacak-Informatika	QUOTE(Nostradamus @ Apr 8 2008, 06:17 PM) U ovom druom mora da bude jednakostranican, jer upisani krug dodiruje trougao u sredistima ivica, i zato sto su odsecci tangenta jednaki. Nostradamus, mislim sta reci, hvala ti puno.....pozzzzz

« Next Oldest · Matematika · Next Newest »

2 User(s) are reading this topic (2 Guests and 0 Anonymous Users)

0 Members: