Računanje broja Pi Monte Karlo metodom

Pre nekoliko dana na predavanju iz Verovatnoće i statistike dotakli smo jednu zanimljivu temu – problem Bifonove igle (Buffon’s needle).

U ravni je dat skup paralelnih pravih, pri čemu je rastojanje između susednih pravih a, a > 0. Na ravan se baca igla dužine l, l < a. Odrediti verovatnoću da igla seče neku od pravih. ("Verovatnoća i statistika za inženjere i studente tehnike", Milan Merkle)

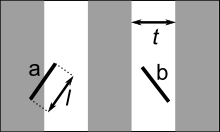U pitanju je običan zadatak iz verovatnoće, ali ono što ga čini posebno zanimljivim jeste činjenica da se na osnovu baš ovakvog bacanja igle može odrediti broj π. Naime, zbog različitih uglova pod kojima igla može da se nađe u odnosu na pravu (kao na slici), u formuli za verovatnoću figuriše broj π. Ako znamo njegovu vrednost, možemo odrediti verovatnoću — ali ako je ne znamo, možemo baciti iglu veliki broj puta da bismo dobili verovatnoću, a onda preko nje izračunati π.

Naravno, jasno je da “veliki broj bacanja” uopšte nije lako izvesti. Ako želimo iole preciznije rezultate, nekoliko hiljada teško da će biti dovoljno, pa se mora stremiti ka daleko većim brojevima. Italijanski matematičar Mario Lazzarini je početkom 20. veka izveo ovaj eksperiment sa 3408 bacanja i dobio vrednost 355/113, što je 3.14159292. Za poređenje, vrednost broja π je 3.14159265, odnosno razlikuju se tek na sedmoj decimali. Članak na Wikipedii objašanjava zašto je dobijena ovako precizna vrednost sa malim brojem bacanja, ali nas to trenutno interesuje. Zanemarićemo njegove rezultate, i pokušati lično da izračunamo π uz pomoć kompjuterske simulacije koja nam omogućava da izvršimo milione “bacanja” u samo jednoj sekundi.

Pre nego što krenemo sa programiranjem, malo ćemo izmeniti problem da bismo olakšali njegovu implementaciju, ne umanjujući preciznost. Umesto beskonačne ravni i Bifonove igle, koristićemo kvadrat određenih dimenzija i krug upisan u njega.

Kao što nam je poznato, površina kvadrata stranice 2r je 4r², dok je površina kruga upisanog u isti r²π. Ukoliko znamo obe površine, jednostavnom matematikom možemo izračunati π. Međutim, mi ih ne znamo, pa ćemo morati da ih aproksimiramo. Kao kod Bifonove igle, to ćemo učiniti nasumičnim biranjem tačaka koje pripadaju kvadratu, s tim što ćemo pamtiti koliko je tačaka pripadalo i krugu. Posle dovoljno iteracija, odnosi ukupnog broja tačaka i tačaka u krugu će biti približno jednaki odnosu površina, što ćemo onda upotrebiti da bismo izračunali π.

Kako je ovde u pitanju aproksimacija, logično je da će više bacanja davati bolje rezultate, i poništiti negativan efekat kompjuterski generisanih random brojeva koji nisu zaista nasumični, već pseudo-nasumični. Računanje broja π na ovaj način se zasniva na tome da je podjednaka verovatnoća izbora bilo koje tačke u okviru kvadrata, pa ćemo mi pretpostaviti da nam naš program daje tačke sa uniformnom raspodelom. Iako radimo samo sa celobrojnim koordinatama, pa zapravo ne analiziramo kompletnu površinu kvadrata, zbog velikih vrednost brojeva rezultati bi trebalo da budu dovoljno precizni.

Ovog načina računanja broja π Monte Karlovom metodom sam se setio zbog nekoliko ljudi koji su pohađali seminare u Petnici i kojima je zadatak bio da na ovaj način izračunaju π — jedina razlika je bila u tome što oni nisu koristili računare već papir i pirinač koji su posle prosipanja morali precizno da prebroje. Ovaj način preporučujem samo najupornijima.

Realizacija algoritma, sa druge strane, je veoma jednostavna. U svakoj iteraciji generišemo dve nasumične vrednosti koje nam predstavljaju X i Y koordinatu tačke, i njih koristimo da bismo izračunali da li ona pripada krugu ili ne. U svom kôdu sam radio sa velikim nenegativnim brojevima da bih izbegao korišćenje manje preciznih realnih brojeva, odnosno ostavio ga za sam kraj. Kvadrat je postavljen u donji levi ćošak prvog kvadranta koordinatnog sistema, odnosno obuhvata tačke od (0,0) do (a,a). Formula na kraju algoritma je dobijena preko odnosa površina kruga i kvadrata.

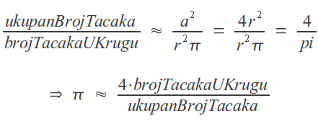
Pošto koristimo random generator, a želimo što veću preciznost, ograničio sam stranicu kvadrata na najveći broj koji možemo dobiti od random generatora, što je u mom slučaju bilo 2³¹-1, odnosno nešto preko dve milijarde. Takođe, da bi se centar kruga nalazio na celobrojnim koordinatama, stranicu kvadrata sam smanjivao na paran broj ukoliko je konstanta RAND_MAX neparna, što bi uglavnom i trebalo da bude slučaj.

Kôd

#include <stdio.h>
#include <stdlib.h>
#include <time.h>

int main()
{
	// Duzina stranice kvadrata

	unsigned long long a = RAND_MAX;

	if (RAND_MAX & 1) // Ukoliko je A neparno
		a--;

	// Poluprecnik kruga

	unsigned long long r = a/2;

	// Brojac tacaka u krugu

	unsigned long long pogodaka = 0;

	// Broj iteracija algoritma, tj. ukupan broj tacaka

	unsigned long long n;

	// Seed za random generator

	srand(time(0));

	// Ucitavamo broj iteracija

	printf("Uneti broj iteracija: ");
	scanf("%lld", &n);

	// Izvrsavamo algoritam

	unsigned long long x, y;
	unsigned long long rr = r*r;

	unsigned long long i;
	for (i = 1; i <= n; i++)
	{
		x = rand();
		y = rand();

		if (x > a || y > a) // Da ne bismo dobijali tacke van kvadrata
		{
			i--; // Ponavljamo iteraciju
			continue;
		}

		if ((x-r)*(x-r) + (y-r)*(y-r) <= rr) // Jednacina kruga
			pogodaka++;
	}

	// Ispisujemo dobijenu vrednost

	double pi = 4 * (double)pogodaka / n;

	printf("Aproksimacija broja Pi: %lf\n", pi);

	return 0;
}

Rezultati

Slede rezultati koje sam dobio testiranjem za različite brojeve iteracija, sve do jednog biliona — za ostalo nisam imao živaca.

1.000 iteracija -> 3,108000
10.000 iteracija -> 3,153600
100.000 iteracija -> 3,144000
1.000.000 iteracija -> 3,140188
10.000.000 iteracija -> 3,141856
100.000.000 iteracija -> 3,141841
1.000.000.000 iteracija -> 3,141715 (50 sekundi)
10.000.000.000 iteracija -> 3,141595 (6 minuta)
100.000.000.000 iteracija -> 3,141595 (sat vremena - bez poboljšanja)
1.000.000.000.000 iteracija -> 3,141594 (deset sati - malo poboljšanje)

Kao što možete videti, što je više iteracija to je precizniji, s tim što broj potrebnih iteracija za povećanje preciznosti stalno raste. Naravno, ponovno pokretanje programa ne bi dalo iste vrednosti, a postoji mogućnost i da se vrednost u nekom trenutku udalji od broja π umesto da mu se približi, ali takva je verovatnoća: ništa nije sigurno, samo verovatno.